Hareket, armonik

Düzenli aralıklarla tıpatıp tekrarlanan harekete, peri­yodik (dönemsel) hareket denir; periyodik hareke­tin en basit türü, armonik (uyumlu, sinüsoidal) hare­kettir. Armonik hareket, çok sık gözlendiği, tanım­lanması ve çözümlenmesi basit olduğu için önemli olmasının yanı sıra, aynı zamanda da herhangi bir armonik hareket, ne kadar karmaşık olursa olsun, bir dizi armonik hareketin toplamı olarak dile getiri­lebildiği için de önemlidir.

Armonik hareketin oluşabilmesi için bulunması gereken iki genel fiziksel nicelikten biri, bir sistemin o anda yapmakta olduğu şeyi yapmayı sürdürme eğilimi olan eylemsizlik (süredurum, atalet), öbürüy- se, sistemi denge durumuna ya da doğal dinlenme durumuna döndürmeye çalışan geriçağırım gücü- dür. Geriçağırım gücünün büyüklüğü, dengeden uzaklaşma (yer değiştirme) miktarıyla doğru orantılıdır; yani sistem dengeden ne kadar uzaklaşmışsa, geriçağırım gücü de o kadar büyük olur. “Esneklik gücü” diye adlandırılan bu tür geriçağırım gücü, ilk olarak XVII. yy’da Robert Hooke tarafından tanımlanmıştır. Esnek geriçağırım gücü ile dengeden uzaklaşma arasındaki orantıya, “Hooke yasası” adı verilir.

Armonik hareketin basit bir örneği, bir yayın ucuna bağlanmış cismin yaptığı harekettir. Yay, CİS- min hareketiyle uzadığı ya da kısaldığı zaman, es- nek geriçağırım gücü uygular; bu da cismin salın- masına neden olur. Cismin kendisiyse eylemsizlik özelliği sergiler; güçler olmasaydı, cisim, tekbiçimii hareket durumunda kalırdı. Dolayısıyla, cismin SO- nuçtaki hareketi, basit armonik harekettir.

Bir elektrik devresinde, bir indükleç (indüktör) ve bir kondansatörden oluşan bileşim, akımın ve volta- jın armonik salınımı için gerekli öğeleri sağlar. İn- dükleç, akım değişikliklerine direnç göstererek ey- lemsizlik oluşturur; kondansatörse, taşımakta olduğu yük miktarıyla doğru orantılı olarak, yüklenmeyi da- ha zorlaştırarak geriçağırım gücü yaratır. Modern elektrikli ve elektronik araçlarda, bu düşünceye da- yanan çok gelişmiş elektrik salmımları elde edilmiş-

Periyodik (dönemsel) hareketin başka bir örneği, basit bir sarkacın, yani uzama özelliği olmayan küt- leşiz bir ipin ucunda sallanan ağırlığın, yaptığı hare- kettir. Yerçekimi geriçağırım gücünü sağlar; ama ağırlığın çizdiği yol bir yay olduğu ¡٢٦¡؟, bu güç, dengeden uzaklaşma miktarıyla doğru orantılı değil- dir; dolayısıyla da bu hareket tam armonik değildir. Yaklaşık 10 dereceye kadar küçük uzaklaşmalar söz konusu olduğunda, hareket armonik diye değerlen- dirilebilir; çünkü sarkacın ideal konumdan aynlma miktarı % 1’den azdır.

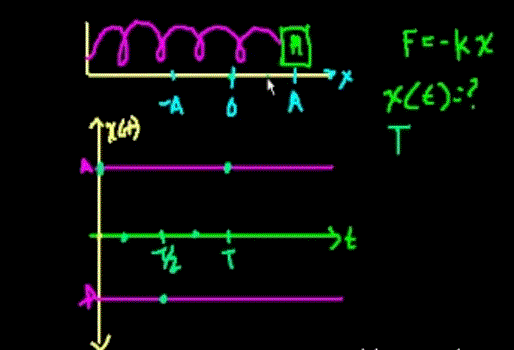
Armonik harekete “sinüsoidal hareket” de denir; çünkü salınan cismin X uzaklaşması ile t zamanı arasındaki matematiksel ilişki bir sinüs (ya da kosi- nüs) fonksiyonudur. Yani, cisim denge durumundan geçerken bir kronometre çalıştırılırsa (f=0), nesne- nin daha sonraki herhangi bir zamanda dengeden uzaklaşması, X = A sin 2 7t ft denklemiyle buluna- bilir; burada ٨ en büyük uzaklaşma, f frekanstır (bir saniyede salınım sayısı). Kronometre, cisim ٨ nok- tasındayken çalıştırılsaydı, hareket, X = ٨ cos 2 K ft denklemiyle gösterilirdi. Ayrıca, cismin hızı ve iv- mesi de, sinüs ya da kosinüs olarak tanımlanabilir.

Basit armonik hareket ile dairesel hareket arasın- da yakın ilişki vardır. Dairesel bir yolda değişmez hızla hareket eden bir cisim, hareket düzleminin içinden izlenseydi (bu durumda daire kenardan gö- rülür), basit armonik hareket kurallarına uyarak, düz bir çizgi üstünde ileri geri hareket ediyormuş gibi görünürdü. Bu nedenle, dairesel bir yol, birbirine dik olarak etki yapan iki geriçağırım gücünün etki- sindeki bir cismin yolu أط!ج düşünülebilir. Bu güçle- rin ikisinin de frekansı aynıdır ve aynı maksimum uzaklaşmayı sağlar; ama birbirlerine oranla 180  evredışı olur (yani, biri minimuma ulaşırken, öbürü maksimumda bulunur).

Elips biçimi hareket de, birbirinden ayrı iki dikey armonik hareketin sonucu olarak görülebilir. Daire­sel harekette olduğu gibi, bu iki gücün frekansları aynıdır; ama ya maksimum uzaklaşmalar farklıdır ya da evre farkı 180°’den farklı bir değerdir (ya da O⁰‘dir ve bu durumda oluşan yol düz bir çizgidir).

Dairesel ya da elips biçimi hareketin iki ayrı ar­monik hareket aracılığıyla tanımlanması çoğunlukla gereksiz olmasına karşın, daha karışık biçimleri, özellikle de Lissajous biçimleri adı verilen biçimleri ele almanın en basit yöntemi genellikle budur.

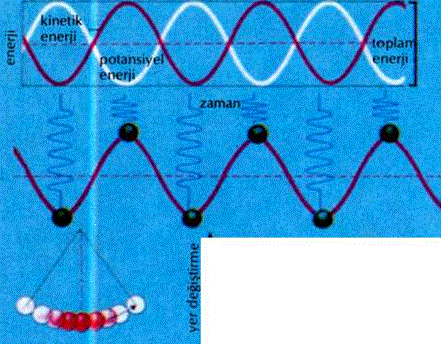
Armonik hareketin belirgin özelliği, denge konu­mu çevresinde bakışımlı harekettir. Her maksimum uzaklaşma, bir öncekinden biraz daha azsa, hare­ketin “sönmekte” olduğu söylenir. Sönme, sarkacın kinetik enerjisi yitimi olayıdır ve titreşimlerin giderek sönmesine neden olur. Enerji soğuran araçlar, söz­gelimi kauçuk yastık gibi basit araçlar, titreşimlerin istenmediği durumlarda kullanılır.

 Dairesel hareket,

Hem doğada, hem de yapay aygıtlarda görülen en yaygın hareket çeşitlerinden biri. Gezegenler Güneş etrafında aşağı yukarı dairesel bir yörüngeyle dö­nerler, Yer’in günlük hareketi yıldızları gökyüzünde dairesel yollarda döner gibi gösterir. Modern sanayi uygarlığının makineleri dairesel çarklara dayanır. Yunan filozofları ve onların görüşlerini benimseyen Ortaçağ’daki skolastik filozoflar dairesel hareketi en kusursuz hareket çeşidi saymışlar, gök cisimlerinin hareketlerinin dairesel olması gerektiğini tartışmışlar­dır. Gezegenlerin gökyüzünde görünen hareketleri açık olarak dairesel olmadığından, İskenderiyeli Pto- lemaios, gezegenlerin genişleyen çemberler halin­deki noktalar çevresinde dairesel hareketine daya­nan karmaşık bir deneysel model hazırlamıştır.

Hareket eden bir cisim dış etkilerden bağımsızsa, bir doğru boyunca değişmez bir hızla hareket et­meyi sürdürür. Bu cisim, hıza sürekli olarak dik ka­lacak biçimde, sürekli olarak doğrultusu değişen bir güç uygulanırsa, bir daire çevresinde yol alır. Söz konusu dik güce “merkezcil güç” adı verilir. Dönen maddenin hızı her zaman teğet olduğundan mer­kezcil güç radyaldır; m kütleli bir cismin dairesel bir yörüngede, değişmez ٧ hızıyla yol alması için merkezcil gücün mv²/ı’ye eşit olması gerekir. Ge­zegenler için merkezcil gücü yerçekimi sağlar.

Daire biçiminde hareket eden bir cismin bir tam devri için gereken zamana periyod (7) denir. Birim zamandaki devirse frekans (f) diye adlandırılır ve T=1/f olur. Radyan/saniye birimindeki ،o açısal hızı ■؛?;rf’ye eşittir, burada ٢, devir/saniye biçiminde veri­lir. Teğet hız ٧, co/’ye eşittir. Bu tanımlamalar ve formüller temel devir verilerini hesaplamada kulla­nılabilir.

Doğrusal hareketin (Bk. HAREKET, DÜZLEMSEL) ölçülerinin dairesel hareketle benzerlikleri var­dır.Doğrusal yer değiştirme (x) açısal yerdeğiştirme- ye (0),doğrusal hız (٧) da açısal hıza (٠٠) karşılık ge­lir. Dönen maddenin eylemsizliğine, “eylemsizlik momenti (/) adı verilir; r yarıçaplı bir daire içinde hareket eden m kütleli bir noktasal cisim için Hmr²‘dir. Doğrusal moment (mv), açısal momente (/،o) karşılık gelir. Bir noktasal cisim için lo)=(mr²)ıa=mvr’d\r. Dairesel kinetik enerji ^,¿²(،)/؛^,dir.

Değişmez hızla dairesel hareket eden bir cismin bir eksen üstüne izdüşümü özel bir salınım türü olan basit armonik hareketi verir (Bk. HAREKET, AR­MONİK).

hlareket, düzlemsel

Hareketin sezgisel bir tanımı “zaman içinde sürekli bir değişme” olmuştur.Benzer bir tanım, genel bir değişiklik kuramını açıklamanın büyük bir sorun oluşturduğu Eskiçağ Yunan filozofları tarafından kul­lanılmıştır. Elea’lı Zenon (İ.Ö. 490-İ.Ö 430) ok para­doksunu ortaya koymuştur: Uzayda yer kaplayan bir cisim durağan haldeki hacmine eşittir; yol al­makta olan bir ok, her an uzayda hacmine eşit bir yer kaplar;dolayısıyla her an ok hareketsizdir. Bu paradoks XVII. yy’a kadar çözülememiştir.

Klasik mekanikte hareketin tanımı matematiğe başvurmayı gerektirir. Hareketi sistemli olarak çö­zümleyebilmek için, hız ve ivme kavramlarına ince­likli tanımlamalar getirilmesi gerekir; bu nicelikler için değerler, bir cisim için her an biliniyorsa, izle­diği bütün yol belirlenebilir. Bu yolla, atomların ha­reketinden gezegenlerin hareketine kadar pek çok hareket problemi çözülebilir.

HIZ

Bir cismin hızı, belirli bir zaman içinde aldığı yolla hesaplanabilir. Yer değiştirmenin zaman farkına bö­lümüne “ortalama hız” denir, metre saniye (m/sn) ya da kilometre saat (kilometre/sa) gibi birimlerle verilir.Belirli bir zaman aralığında bir cismin ortala­ma hızı, bu zaman aralığında cismin tam olarak ne kadar yol aldığı konusunda da kabaca bir bilgi ve-

Zaman içinde belirli bir an için ٧ hızını (anlık hız) elde etmek için, bölünemeyecek kadar küçük bir dt anındaki bölünemeyecek kadar küçük dr yer değiştirmesi bilinmelidir; böylece v=dr/dt olur.

Hız vektöre! bir nicelikt؛r;hem doğrultusu, hem de bir büyüklüğü vardır. Bir cismin hızı aynı doğrul- tuda ve değişmez bir değerde kalırsa, cisim doğru- sal hareket etmektedir.Bu hareket çok yaygındır: Uçak, tren ve gemiler belirli bir hıza ulaştıktan son- ra, değişmez bir hızda ve rotaları uygunsa değiş- mez bir doğrultuda ilerlerler, Doğrusal hareket, do- ğada herhangi bir net güç uygulanmadan sağlanabi- len tek hareket olduğundan, özeldir, □oğrusal ha- reket eden bir araçtaki yolcu ne koltuğuna gömü- !□٢, ne de herhangi bir yana sarsılır. Bu yüzden ta- ^macılıkta doğrusal hareket yeğ tutulur.

İVME

Birbirini etkisiz duruma getirmeyen güçler bir cisme etkidikleri zaman, doğrusal hareket sona erer. ¥al- nızca hızın doğrultusunda bir hız değişikliği olursa, ivme kuramı konusunda basit bir fikir edinilebilir. İvme, genellikle bir saniyede gerçekleşen hız değ¡- آخ؛ا>ا؛ؤ (m/sn) biçiminde dile getirilir, Duruş halinden 72 km/sa (20 m/sn) hıza ٦٠ saniyede ulaşan bir otomobilin ivmesi 2 m/sn؛’dir. ivrifelenmeye yol açan güç, motor tarafından üretilir ve sürücü aynı ivmelendirici güçle koltuğa yapışır. Negatif bir ivme (hız düşmesi) arabayı yavaşlatır. Kişinin emniyet ke- meriyle güvenliği sağlandıkça negatif güç etkimez ve sürücünün ileri hareketi sürer.

İvme aynı zamanda bir vektördür, ivmelenmeye neden olan güç, hızla aynı doğrultuda etkimiyor- sa,ivme birbirine dik iki bileşene ayrılabilir. Hız doğrultusundaki ivmeye “teğet ivme” (a؛) adı verilir. Ortalama teğet ivme, birim zamanda hızdaki değiş- meye eşittir: a,=v/،.

Hıza dik olan ivme bileşenine “radyal ivme” (ود adı verilir; v-’/r’ye eşittir; burada r, cismin ele alınan zamanda yol aldığı dairesel yörüngenin yarıçapıdır (düşsel ya da gerçek). Bir mermi yolu her zaman birbirine bağlanmış, küçük dairesel yörüngeler ola- rak ele alınabilir ve çemberin ٢ yarıçapı, yolun her noktasında farklı olabilir. Cisim doğrusal harekette bulunsa bile radyal ivme dolayısıyla hareketi eğri olacaktır.

KONUMUN HESAPLANMASI

Bir doğru boyunca doğrusal hareket eden cismin kesin durumu x=؛/؛ denklemi kullanılarak kolayca hesaplanabilir. Burada X aşılan uzaklıktır. Formülün sağ ve sol yanında aynı birimler kullanılmalıdır; yani hız kilometre saat (km/sa) olarak verilmişse, zaman saat, uzaklık da kilometre biriminde olmalıdır; hız metre saniyeyse (m/sn) zaman saniye, uzaklık da metre olmalıdır.

□uruş konumundan değişmez bir ivmeyle hare- kete başlayan bir cismin hızı da ءة=ما formülünden hesaplanabilir. Burada da hesaplamalar metre sani- yeyle ya da seçenek olarak kullanılacak ölçü birim- leriyle yapılmalıdır.

Doğrusal ivmeli hareket, cismin aynı oranda de- ğişmez bir ivmenin (yerçekimi gibi) etkisinde kaldığı zaman oluşan harekettir. Böyle bir cismin hareketi x= ¹halد formülüyle hesaplanır. Dolayısıyla, aşılan uzaklık, zamanın karesiyle değişir. Söz konusu Cİ- sim ivmelenme başlamadan önce de zaten hareket halindeyse, bu zaman aralığında aşılan uzaklık için V’₀i de işleme katılmalıdır ve X = v_at + at^.formülüy- le işlem yapılır, ilk hızın ivmeyle aynı doğrultuda olması gerekmemektedir. Böyle bir durumda Ivjı’ye eşit uzaklık bir doğrultuda,’aynı zamanda ‘/؛a،؛’ye eşit bir uzaklık da, öbür doğrultuda aşılmaktadır.

DÜŞME HAREKETİ

Cismin doğrusal ivmeli harekette bulunduğu en çok bilinen durum, Yer’in yerçekimi alanına bırakıldığı zaman (düştüğü zaman) görülür. Böyle bir cismin hızı her saniyede 9,8 .m/sn artar. Yerçekimi gücü­nün ivmesi aslında değişmez değildir; ama 30 km yüksekliğe kadar bu değerdeki sapmalar % 1’den küçüktür. Düşen bir cisim yer yüzeyine bir doğru boyunca iner ve aynı zamanda, yerçekimi nedeniy­le oluşan ivmeli düşey harekette bulunur.Bu iki ha­reketin bileşkesi olan durum, artık bir doğru değil­dir ve ileriye oranla aşağı doğru artan uzaklıklarda gerçekleşir; dolayısıyla parabol biçimi bir yol oludu.

Düşmekte olan bir cismin belirli bir t süresi son­raki konumu, metre boyutunda yüksekliğe (h), ön­ceki formülden, başlangıç yüksekliği de eklenerek hesaplanabilir: h: h= v„t – ‘/.9.8)؛)K Formüldeki son öğeden dolayı cisim sürekli olarak alçalacak ve so­nunda yere çarpacaktır. Bu süre içinde aştığı yatay uzaklık v_r<t’dir. Düşey ilk hız (٧„), yatay ilk hızdan (٧„) farklıdır. Bu hesaplamaya havanın direnci ve öbür güçler katılmamıştır.

h yüksekliğinden bırakılan maddenin yere çaptı­ğı andaki düşey hızı, aynı zamanda maddenin yu­karı doğru atıldığında, h yüksekliğine çıkması için gerekli hızı verir. Yüksek hızlarda hava direnci, dü­şüş oranında son bir artış sağlar. (Ayrıca Bk. HARE­KET YASALARI.)