DİKGEN sıf. (dik ve —gen’den). Mat. Bir-biriyle veya kesim noktasındaki teğetleriyle, dik açı yapacak şekilde kesişen: Dikgen doğrular. Dikgen eğriler. Esk. Kaim. || Dikgen doğrular, doğrultuları uzayda dik açı yapan doğrular. (Bu doğrular, ayrıca birbirini kesiyorsa, bunlara dik doğrular denir.) || Dikgen eğriler, bir ortak noktadaki teğetleri arasında dik açı olan eğriler: Dikgen çemberler. || Dikgen eksenler, aralarında bir dik açı yapan eksenler. || Dikgen izdüşüm, izdüşüm düzlemine veya eksenine çıkılan dikmelere göre alınan izdüşüm. || Dikgen koordinat sistemi, koordinat eksenleri dik olan karşılaştırma sistemi. || Dikgen küreler, bir ortak noktada teğet olan düzlemleri arasında dik açı olan küre-
315
dikenli uyuşturan balığı
dikilitaşlar
a— Heliopolis, Mısır b— Circo Massimo Roma c— Luksor, Paris
dikilitaşlar
Orta krallık Mısır
altta solda,
Gudea Yeni sümer devr Louvre müzesi, Paris
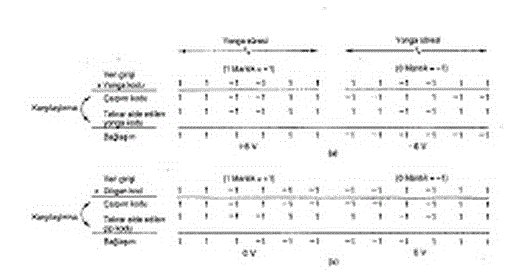
ler. || Dikgen matris, her satırındaki elemanların kareleri toplamı birime eşit olan ve ayrı iki toplamı sıfır olan bir A kare matrisi. (Bk. ANSiKL.) || Dikgen normlıı, eksenleri birbirine dik ve birim vektörlerinin uzunlukları aynı olan bir koordinat sistemi için kullanılır. || Dikgen simetri, birbirine simetrik herhangi iki noktayı birleştiren doğruların, simetri düzlemine veya eksenine dik olduğu simetri. || Dikgen üç-yüzlü, bütün yüzleri arasındaki açıları dik olan üçyüzlü. || Dikgen vektörler. ortonorm-lu bir tabanı olan, n boyutlu bir vektörel uzayda,
.tj, X”, …, x„ ve yı, y2, y„ bileşenleri,
xı yı + x» y2 + … -\-Xnyn — o
^ Asarhaddon Asur (M.Ö. VII. yy.)
Berlin müa
Bıçakçının mezar steli
Vatikan müzesi, Roma
bağıntısını^sağlayan, yani iç çarpımı sıfır
olan U ve V vektörleri. (Bk. ANSiKL.) || üçlü dikgen sistem, ortak noktalarının her birinde, teğet düzlemli bir dikgen üçyüzlü meydana getiren üç yüzey kümesinden kurulmuş sistem.
— ANSİKL. Mat. Dikgen matrisler, n inci basamaktan A [flii] kare matrisi verilmiş olsun. Tanımda verilen özellikler söyle gösterilir:
V i, aru -f- a2iz 4- … -f- a2in — 1;
eğer
i # atı an + a,2 a,2 + … + a,„ a,„ = 0 jse Kronecker’in işaretleri kullanıldığında
suz fonksiyonlar dizisi gözönüne alındığında, p = q olmamak şartıyle p ve «’nün değeri ne olursa olsun, bu fonksiyon dizisi için
r:
<Pp(x) <p,(î) dx
bağıntısı sağlanabiliyorsa, bu dizi (a, b) aralığında bir dikgen fonksiyonlar ailesi meydana getirir.
Böylece cos px (p = 0, 1, 2, …) ve sin qx (q = 1, 2, …) fonksiyonlarından meydana gelen fonksiyon ailesi; 2 71 genişliğindeki bütün aralıklarda dikgendir.
Dikgen bir fonksiyon ailesi, fc’nın her değeri için
uzes
Mezar steli
Etruria
aşağıda,
Hegeso mezar steli (M.Ö. IV.yy.)
Atina, Dipylon, Yunanistan
T* J • . OİUr-
□ undan başka, matrisi meydana getiren satır vektörlerinin norm durumuna getirildikleri ve ikişer ikişer birbirine dikgen oldukları söylenebilir.
Dikgen matrislerin daha başka özellikleri ile yukarıda sayılan özellikleri arasında mantık açısından uygunluk olduğu açıkça ispatlanabilir.
1) D, A’mn determinantı, de a<i ‘nin kofaktörü ise, i ve /’nin bütün değerleri için
„ r>7
‘<ı=-’dir.
D
2) A ile evriği ‘A ’mn çarpımı matris birimi I’ye eşittir. Bu da, A matrisinin düzgün bir matris ve 1A ’nin da A-1 ters matrisine eşit olduğunu gösterir.
3) Satırlarla ilgili özellikler sütunlara da uygulanır; n basamaklı bir dikgen matris normlandırılmış ve ikişer ikişer birbirine dikgen n matristen meydana gelmiştir. Aynı basamaktan iki matrisin dikgen çarpımı dikgen bir matristir. Değişli olmayan n basamaklı dikgen matrisler bir grup meydana getirir. Bir matris dikgen ise, evriği, tersi, ek matrisi ve bütün kuvvetleri de dikgendir. Bir sanal matris dikgen ise, eşlenik matrisi de dikgendir.
Dikgen matrisler arasında bazılarının determinantı + 1 dir: bunlara dikgen doğru matrisler denir. Bazılarının determinantı ise — 1 dir: bunlara da dikgen aykırı matrisler denir.
Dikgen matrisler, tabanların değiştirilmesinde önemli rol oynar. Aynı problemin değişik bir türü olan çizgisel uygulamalarda da dikgen matrislerin rolü büyüktür.
Böylece, ortonormlu eksenlerle donatılmış bir düzlemde.
olursa, (a, b) aralığında «normalleştirilmiş» olur.
sin 1ix [p, q = 1, 2, 3, …]
1 1
,—= COS px, —- :
V2* V 2ıx
dikgen fonksiyon ailesi 2 r. genişliğinde bütün aralıklarda normalleştirilmiştir.
• Bir fonksiyonun dikgen fonksiyon serisi halinde açılması. Bir (a, b) aralığında tanımlı olan ve integrali alınabilen bir f(x) fonksiyonu ve bu aralıkta dikgen olan bir ¥ k(x) fonksiyonlar ailesi verildiğine göre, f(x) bazı koşullar sağladığı zaman bu fonksiyon (a. b) aralığında, <i> k(x) fonksiyonlarının
J(x)= a0(pü(x) + at^(x) -f …-{- a„(p„(x) +…..,
yakınsak serisi halinde göstermek mümkündür. an, 01, …, n,„ katsayıları sabit sayılardır. Bu durumda f (x) fonksiyonu dikgen fonksiyon serisi halinde açılmıştır. (a, b) aralığında Vt(x) fonksiyonlarının dikgen olmasından ötürü.
f /(■*) <ft(x) dx
7.
-, k = 0, 1, 2,
. _ T cos 6 sin 81 L—sin 0 cosej
dikgen doğru matrisi, ( e ) açılı bir dönmeyi gösterir.
[cos ( sin 6
sin 61 — cos 0J
aykırı dikgen matrisi de bir doğru etrafın, « ..
da — argumanh bir dönmeyi gösterir.
2
Genellikle, dikgen matrisler bir izometriyi tanımlar.
A bir dikgen matris olmak üzere, kA şeklindeki bir matris, bir izometri ile bir benzerliğin çarpımını tanımlar.
• Dikgen vektörler. Bu vektörler arasındaki tanım bağıntısı, üç boyutlu geometride bilinen bir formülü genelleştirir Bağıntıdan çıkarılan sonuç, dikgen ortonormlu bir tabana uygulanır; bu tabanın değiştirilmesi halinde, yeni taban da dikgen ortonormlu olmak zorundadır (dikgen geçişli matris). İki vektörün iç çarpımının tabana bağlı olmaması için gerekli sart bu-dur. Böylece vektörel uzayda, tabanla bağıntısı olmayan bir ölçü verilmiş olur. Veri-rilen bir vektöre dikgen vektörler, n—1 boyutlu bir uzay meydana getirir: bugünün geometrisinde bu vektörler, bir düzleme paralel olan bir vektörler cümlesi meydana getirir.
• Dikgen fonksiyon. Bir (a, b) aralığında integrali alınabilen ,P((X) f<pı< = 0, 1, 2. . )son-
olduğu ispatlanır. Genliği 2 r. olan aralıkda bir fonksiyonun Fourier serisi halinde açılması dikgen fonksiyonların seri biçiminde açılımının özel halı olarak görülür. Uygulanan fonksiyon takımı yukarıda işaret edilen cos px (p = 0, 1, 2, …) ve sin qx (q = 1, 2, …) fonksiyonlardan meydana gelmiştir. Dikgenleştirme i. Mat. Bir Eukleides u-zayınm alt cümlesi veya doğrudan doğruya cümlenin kendisi için, ikişer ikişer birbirine dik olan temel eksenlerin araştırılması (LM)





