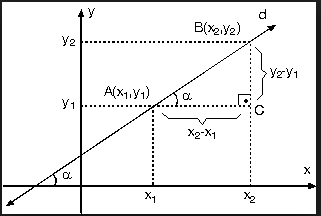
analitik geometri

analitik geometri
Geometri araştırmalarının, cebir yöntemleriyle uygu­
landığı matematik dalı
(koordinatlar geometrisi
de de­
nir). Temel olarak problemleri düzlem geometrisi için­
de araştırmaya yönelik tasarlanmasına karşın (iki boyut­
lu düzlemde geometri), analitik geometri, daha yüksek
boyuttaki uzayların incelenmesinde de kullanılabilir.
Düzlem analitik geometrisi, konik kesitlerin sistemli bi­
çimde incelenmesini içerir. Üç boyutun analitik geo­
metrisi, “katı cisimler analitik geometrisi” diye adlandı­
rılır ve dörtyüzlü alanların incelenmesini içerir.
Analitik geometride, noktaların konumları uygun sa­
yı gruplan (koordinatlar) aracılığıyla belirtilir; böylece,
noktalar arasındaki geometrik ilişki, koordinatları ara­
sındaki cebir ilişkisiyle eşdeğerli olur. Cebir ile geometri
arasındaki bu uygunluk nedeniyle, çoğunlukla geomet­
rik ilişkileri kapsayan önermeler, cebir ilişkileri kullanı­
larak kanıtlanabilir. Bu tür cebir tekniklerinin, kuramsal
geometri yöntemlerini uygulamada ortadan kaldıracak
derecede etkili oldukları kanıtlanmıştır.
TARİHÇE
Analitik geometrinin temellen XVII.yy’da Fransız filo­
zofu ve matematikçisi René Descartes tarafından atıl­
mıştır. Descartes, analitik geometrinin temel ilkelerini
felsefe tarihi açısından önemli bir yapıt olan ve kiliseyle
herhangi bir tartışmadan kaçınmak amacıyla adını koy­
madan yayınladığı
Metot Üzerine Konuşmalar
(Discurs de la méthode, 1637) adlı yapıtında açıklamıştır. Pi­
erre de Fermât da analitik geometri yöntemleri üstünde
çalışmış, ama bu konuyla ilgili kitabı, 1679’a kadar ya­
yınlanmamıştır. Analitik geometrinin günümüzdeki bi­
çimiyse, daha sonra Leonhard Eulertarafından geliştiril­
miştir.
Analitik geometri yöntemlerinin doğuşu ve bu­
nun sonucu olarak hesap yöntemlerindeki ilerleme,
matematikte, klasik matematikten yeni bir çağa geçişi
belirtir. Analitik geometrinin bulunması, aksiyomların
kullanımına dayanan klasik Yunan geometrisinin gelişti­
rilmesinde önemli bir adım olmuştur.